سلام، بنده تقریباَ تونستم چیزی شبیه به فایل شما رو آماده کنم. امیدوارم مفید باشه.
کد رو در قسمت زیر براتون گذاشتم.
\documentclass[10pt,fleqn]{article}
\usepackage{amsmath}
\usepackage{amsfonts,tabularx}
\usepackage{amssymb}
\usepackage[paperwidth=8.27in,paperheight=11.69in,margin=2cm]{geometry}
\usepackage{array,multirow,tikz,enumitem}
\usepackage{xepersian}
\settextfont[Scale=1.2]{Yas}
\setmathdigitfont[Scale=1.2]{Yas}
\linespread{1.8}
\newcolumntype{p}{>{\raggedright\arraybackslash}m{3cm}}
\newcolumntype{q}{>{\raggedleft\arraybackslash}m{3cm}}
\newcolumntype{n}{>{\raggedleft\arraybackslash}m{14.58cm}}
\begin{document}
\centering
بسمه تعالی
\begin{tabular}{|q|q|q|q|q|}
\hline
\multicolumn{5}{|c|}{اداره آموزش و پرورش استان} \\
\hline
مشخصات دانشآموز & مشخصات امتحان & زمان امتحان: & دبیرستان: & نمره مستمر: \\
\hline
نام: & درس: & تاریخ: & نوبت امتحان: & نمره کتبی: \\
\hline
نامخانوادگی: & پایه: & ساعت امتحان: & سال تحصیلی: & نام دبیر: \\
\hline
\end{tabular}
\begin{tabular}{|c|n|c|}
\hline
ردیف & \multicolumn{1}{c|}{صفحه اول} & بارم \\
\hline
1 & تابع $y=(x+1)^3$ را رسم کنید. & 1/5 \\[2cm]
\hline
2 & نمودار تابع
$f(x)=
\begin{cases}
x^2 & x\geq -1\\
2 & x<-1
\end{cases}$
را رسم کنید. در چه فاصلههایی این تابع صعودی و در چه فاصلههایی نزولی است؟ & 1 \\[2cm]
\hline
3 & عبارت $x^6-1$ را یک بار برحسب $x-1$ و یک بار برحسب $x+1$ تجزیه کنید. & 2\\[2cm]
\hline
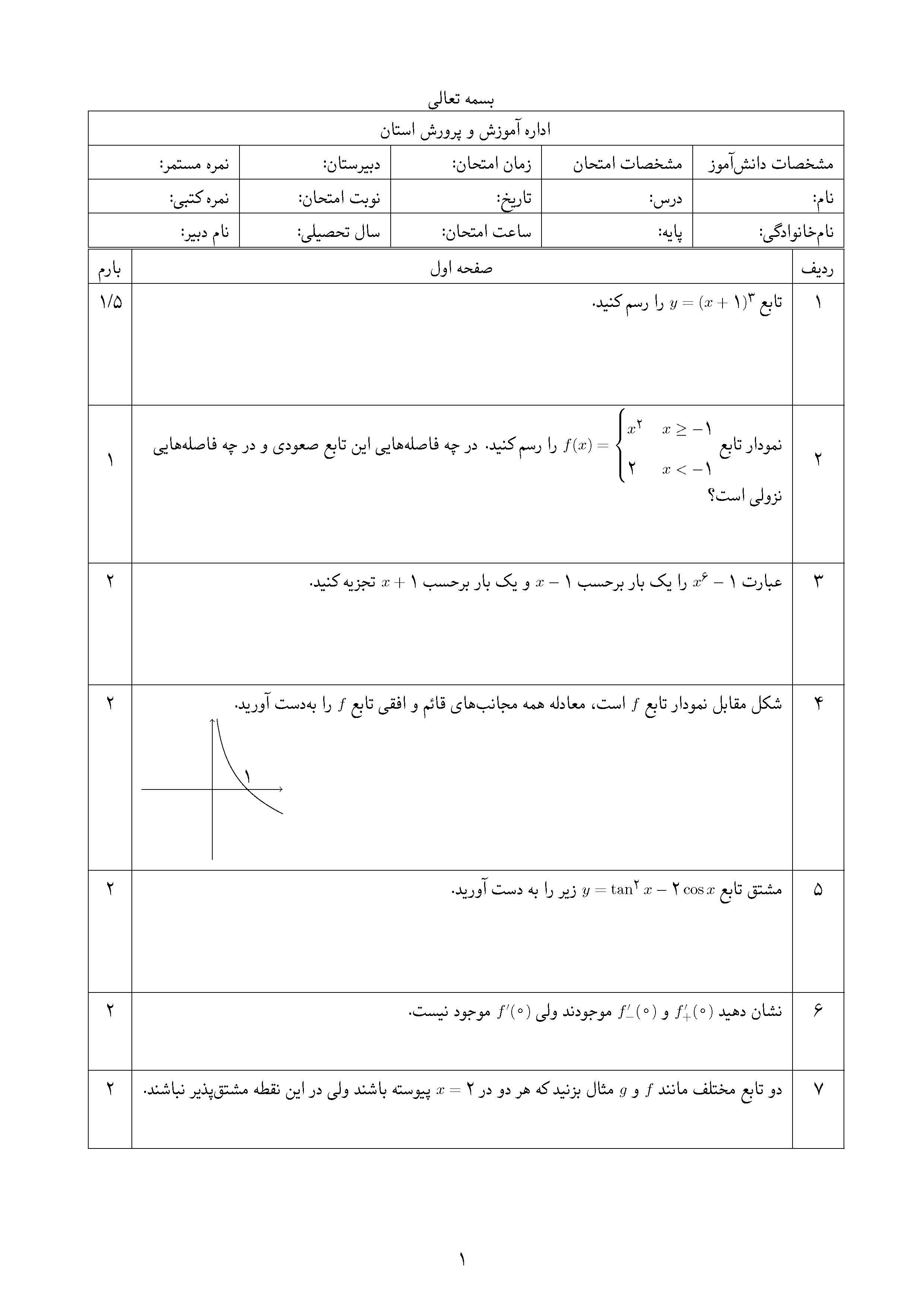
4 & شکل مقابل نمودار تابع $f$ است، معادله همه مجانبهای قائم و افقی تابع $f$ را بهدست آورید. & 2 \\
&\hfill
\begin{tikzpicture}[scale=0.8]
\draw[->] (-2,0) -- (2,0);
\draw[->] (0,-2) -- (0,2);
\draw[black,rotate=270,domain=-2:0.7,samples=500] plot (\x,{exp(\x)});
\draw (1,0) node [above] {1};
\end{tikzpicture}
& \\[1cm]
\hline
5 & مشتق تابع $y=\tan^2x-2\cos x$ زیر را به دست آورید. & 2 \\[2cm]
\hline
6 & نشان دهید $f_{+}'(0)$ و $f_{-}'(0)$ موجودند ولی $f'(0)$ موجود نیست. & 2 \\[1cm]
\hline
7 & دو تابع مختلف مانند $f$ و $g$ مثال بزنید که هر دو در $x=2$ پیوسته باشند ولی در این نقطه مشتقپذیر نباشند. & 2\\[1cm]
\hline
\end{tabular}
\newpage
\begin{tabular}{|c|n|c|}
\hline
ردیف & \multicolumn{1}{c|}{صفحه دوم} & بارم \\
\hline
1 & تابع $y=(x+1)^3$ را رسم کنید. & 1/5 \\[2cm]
\hline
2 & نمودار تابع
$f(x)=
\begin{cases}
x^2 & x\geq -1\\
2 & x<-1
\end{cases}$
را رسم کنید. در چه فاصلههایی این تابع صعودی و در چه فاصلههایی نزولی است؟ & 1 \\[2cm]
\hline
3 & عبارت $x^6-1$ را یک بار برحسب $x-1$ و یک بار برحسب $x+1$ تجزیه کنید. & 2\\[2cm]
\hline
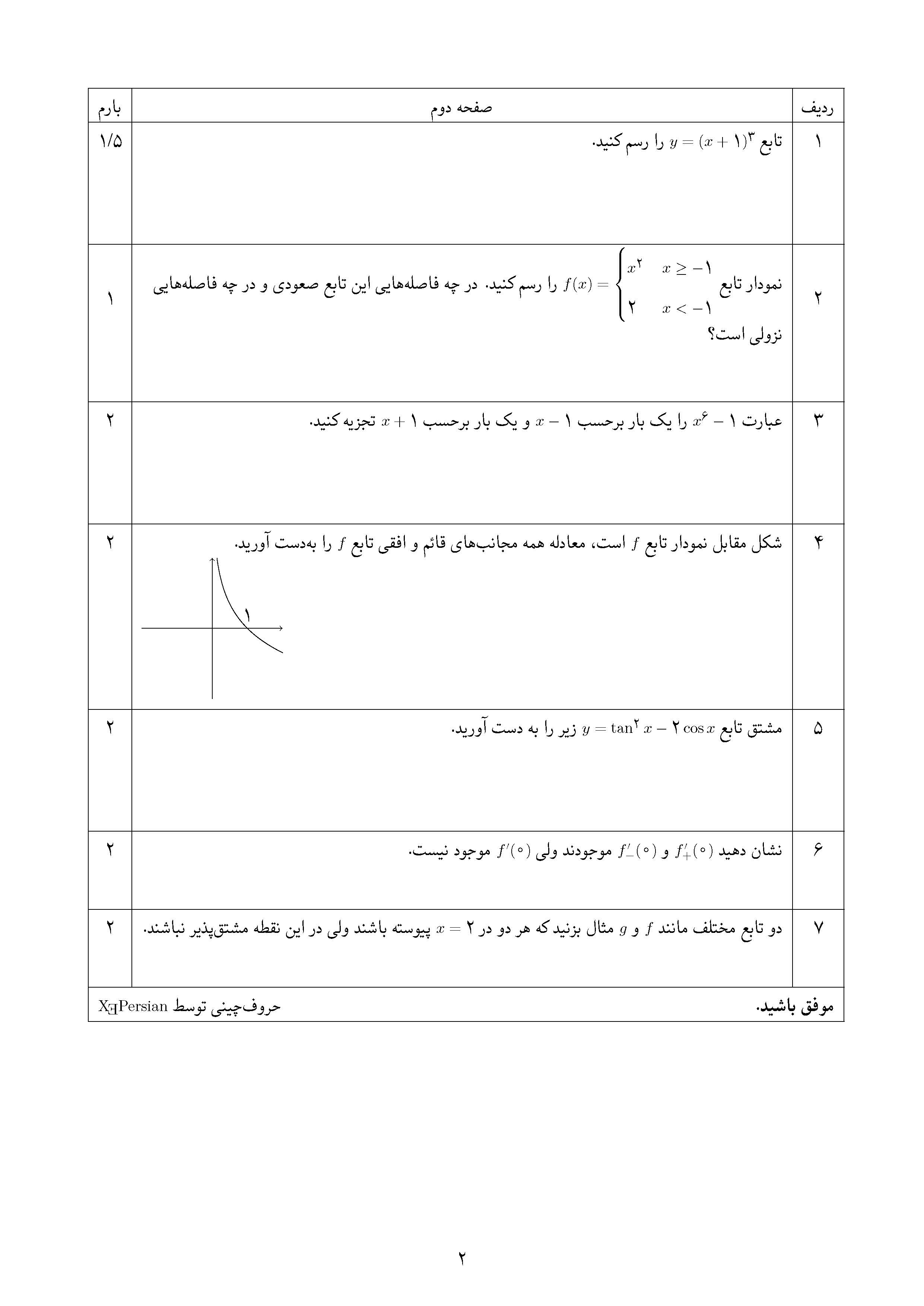
4 & شکل مقابل نمودار تابع $f$ است، معادله همه مجانبهای قائم و افقی تابع $f$ را بهدست آورید. & 2 \\
&\hfill
\begin{tikzpicture}[scale=0.8]
\draw[->] (-2,0) -- (2,0);
\draw[->] (0,-2) -- (0,2);
\draw[black,rotate=270,domain=-2:0.7,samples=500] plot (\x,{exp(\x)});
\draw (1,0) node [above] {1};
\end{tikzpicture}
& \\[1cm]
\hline
5 & مشتق تابع $y=\tan^2x-2\cos x$ زیر را به دست آورید. & 2 \\[2cm]
\hline
6 & نشان دهید $f_{+}'(0)$ و $f_{-}'(0)$ موجودند ولی $f'(0)$ موجود نیست. & 2 \\[1cm]
\hline
7 & دو تابع مختلف مانند $f$ و $g$ مثال بزنید که هر دو در $x=2$ پیوسته باشند ولی در این نقطه مشتقپذیر نباشند. & 2\\[1cm]
\hline
\multicolumn{3}{|l|}{\textbf{موفق باشید.} \hfill حروفچینی توسط \lr{\XePersian}}\\
\hline
\end{tabular}
\end{document}