سلام
فرمول شما به قدری طولانی هست که من حتی عرض صفحه رو حدود ۳ برابر کردم و فونت را هم کوچکتر کردم و جا نشد.
روش شکستن ماتریس بصورت ساده کدش باید به این صورت بنویسین.
برای اینکه کد درایهها شلوغ بود و Indent دادن در این قسمت پاسخ سایت خوب کار نمیکنه،
من به جای درایههای شلوغ ماتریستون، اون اعداد رو نوشتم که ساده و قابل فهمتر باشه که آرایهها رو چطور چیدم.
در کد، %%%%%%%%%%%%%%%%%%%%%%%%% یعنی هر ارایه تموم شده.
\documentclass[twocolumn,12pt]{article}
\usepackage{amsmath}
\begin{document}
\begin{align}
&\left[\begin{array}{l}
11\\
12\\
13\\
14
\end{array}
\right.
\nonumber\\%%%%%%%%%%%%%%%%%%%%%%%%%
&\quad\begin{array}{l}
21\\
22\\
23\\
24
\end{array}
\nonumber\\%%%%%%%%%%%%%%%%%%%%%%%%%
&\quad\begin{array}{l}
31\\
32\\
33\\
34
\end{array}
\nonumber\\%%%%%%%%%%%%%%%%%%%%%%%%%
&\quad\left.\begin{array}{l}
41\\
42\\
43\\
44
\end{array}\right]
\left[\begin{array}{l}
a_{1}\\
a_{2}\\
a_{1}^{\prime}\\
a_{2}^{\prime}\\
\end{array}\right]=
\nonumber\\%%%%%%%%%%%%%%%%%%%%%%%%%
&\left[\begin{array}{l}
51\\
52\\
53\\
54
\end{array}\right]
\end{align}
\end{document}
خروجی:
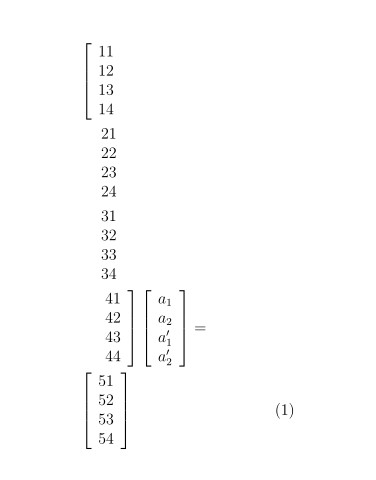
و برای تمام عرض کردنش راههای زیادی هست، (چون در پرسش مشخص نکردین دوستونی چه جوری شده؛ در documentclass دوستونی شده، یا با بسته multicol و ...، و چون بعضی راهها در همه جواب نمیدن من راهی رو میگم که در هر همه حالتها اغلب جواب میده)
دقت کنین دو بسته زیر را فراخوانی باید فراخوانی بشه.
\usepackage{cuted}
\usepackage{flushend}
(بستهی دوم اجباری نیست)
در نهایت، با وارد کردن کد ماتریس شما در نمونهی بالا:
\documentclass[twocolumn,12pt]{article}
\usepackage{geometry}\geometry{margin=2cm}
\usepackage{lipsum}
\usepackage{cuted}
%\usepackage{flushend}
\usepackage{amsmath}
\begin{document}
\lipsum[1]
\begin{strip}
\begin{align}
& \left[\begin{array}{l}
i \kappa_{x}+\frac{1}{2}\kappa_{0}(\chi_{\mathrm{me}}^{xx} \kappa_{y}-\chi_{\mathrm{me}}^{xy} \kappa_{x})+ \frac{1}{2}h_{1}(\chi_{\mathrm{mm}}^{xx} \kappa_{x}+\chi_{\mathrm{mm}}^{xy} \kappa_{y})
\\
i \kappa_{y}+\frac{1}{2}\kappa_{0}(\chi_{\mathrm{me}}^{yx} \kappa_{y}-\chi_{\mathrm{me}}^{yy} \kappa_{x})+ \frac{1}{2}h_{1}(\chi_{\mathrm{mm}}^{yx} \kappa_{x}+\chi_{\mathrm{mm}}^{xy} \kappa_{y})
\\
\kappa_{y}h_{1}-\frac{1}{2}i\kappa_{0}(\chi_{\mathrm{ee}}^{xx} \kappa_{y}-\chi_{\mathrm{ee}}^{xy} \kappa_{x})- i\frac{1}{2}h_{1}\kappa_{0}(\chi_{\mathrm{em}}^{xx} \kappa_{x}+\chi_{\mathrm{em}}^{xy} \kappa_{y})
\\
-\kappa_{x}h_{1}-\frac{1}{2}i\kappa_{0}(\chi_{\mathrm{ee}}^{yx} \kappa_{y}-\chi_{\mathrm{ee}}^{yy} \kappa_{x})- i\frac{1}{2}h_{2}\kappa_{0}(\chi_{\mathrm{em}}^{yx} \kappa_{x}+\chi_{\mathrm{em}}^{yy} \kappa_{y})
\end{array}
\right .
\nonumber \\ %%%%%%%%%%%%%%%%%%%%%%%%%
& \quad \begin{array}{l}
-i \kappa_{x}+\frac{1}{2}\kappa_{0}(\chi_{\mathrm{me}}^{xx} \kappa_{y}-\chi_{\mathrm{me}}^{xy} \kappa_{x})- \frac{1}{2}h_{2}(\chi_{\mathrm{mm}}^{xx} \kappa_{x}+\chi_{\mathrm{mm}}^{xy} \kappa_{y})
\\
-i \kappa_{y}+\frac{1}{2}\kappa_{0}(\chi_{\mathrm{me}}^{yx} \kappa_{y}-\chi_{\mathrm{me}}^{yy} \kappa_{x})- \frac{1}{2}h_{2}(\chi_{\mathrm{mm}}^{yx} \kappa_{x}+\chi_{\mathrm{mm}}^{yy} \kappa_{y})
\\
\kappa_{y}h_{2}-\frac{1}{2}i\kappa_{0}(\chi_{\mathrm{ee}}^{xx} \kappa_{y}-\chi_{\mathrm{ee}}^{xy} \kappa_{x})+ i\frac{1}{2}h_{2}\kappa_{0}(\chi_{\mathrm{em}}^{xx} \kappa_{x}+\chi_{\mathrm{em}}^{xy} \kappa_{y})
\\
-\kappa_{x}h_{2}-\frac{1}{2}i\kappa_{0}(\chi_{\mathrm{ee}}^{yx} \kappa_{y}-\chi_{\mathrm{ee}}^{yy} \kappa_{x})+ i\frac{1}{2}h_{2}\kappa_{0}(\chi_{\mathrm{em}}^{yx} \kappa_{x}+\chi_{\mathrm{em}}^{yy} \kappa_{y})
\end{array}
\nonumber \\ %%%%%%%%%%%%%%%%%%%%%%%%%
& \quad \begin{array}{l}
\kappa_{x}\frac{h_{1}}{\kappa_{1}}+\frac{1}{2}ih_{1}(\chi_{\mathrm{me}}^{xx} \kappa_{x}+\chi_{\mathrm{me}}^{xy} \kappa_{y})- \frac{1}{2}i\kappa_{0}(\chi_{\mathrm{mm}}^{xx} \kappa_{y}-\chi_{\mathrm{mm}}^{xy} \kappa_{x})
\\
-\kappa_{x}\frac{h_{1}}{\kappa_{1}}+\frac{1}{2}ih_{1}(\chi_{\mathrm{me}}^{yx} \kappa_{x}+\chi_{\mathrm{me}}^{yy} \kappa_{y})- \frac{1}{2}i\kappa_{0}(\chi_{\mathrm{mm}}^{yx} \kappa_{y}-\chi_{\mathrm{mm}}^{yy} \kappa_{x})
\\
\kappa_{x}\kappa_{1}-i\frac{1}{2}\kappa_{0}h_{1}(\chi_{\mathrm{ee}}^{xx} \kappa_{x}+\chi_{\mathrm{ee}}^{xy} \kappa_{y})+ \frac{1}{2}i\kappa_{0}^{2}(\chi_{\mathrm{em}}^{xx} \kappa_{y}-\chi_{\mathrm{em}}^{xy} \kappa_{x})
\\
\kappa_{y}\kappa_{1}-i\frac{1}{2}\kappa_{0}h_{1}(\chi_{\mathrm{ee}}^{yx} \kappa_{x}+\chi_{\mathrm{ee}}^{yy} \kappa_{y})+ \frac{1}{2}i\kappa_{0}^{2}(\chi_{\mathrm{em}}^{yx} \kappa_{y}-\chi_{\mathrm{em}}^{yy} \kappa_{x})
\end{array}
\nonumber \\ %%%%%%%%%%%%%%%%%%%%%%%%%
& \quad \left .\begin{array}{l}
\kappa_{y}\frac{h_{2}}{\kappa_{2}}-\frac{1}{2}ih_{2}(\chi_{\mathrm{me}}^{xx} \kappa_{x}+\chi_{\mathrm{me}}^{xy} \kappa_{y})- \frac{1}{2}i\kappa_{0}(\chi_{\mathrm{mm}}^{xx} \kappa_{y}-\chi_{\mathrm{mm}}^{xy} \kappa_{x})
\\
-\kappa_{x}\frac{h_{2}}{\kappa_{2}}-\frac{1}{2}ih_{2}(\chi_{\mathrm{me}}^{yx} \kappa_{x}+\chi_{\mathrm{me}}^{yy} \kappa_{y})- \frac{1}{2}i\kappa_{0}(\chi_{\mathrm{mm}}^{yx} \kappa_{y}-\chi_{\mathrm{mm}}^{yy} \kappa_{x})
\\
-\kappa_{x}\kappa_{2}+i\frac{1}{2}\kappa_{0}h_{1}(\chi_{\mathrm{ee}}^{xx} \kappa_{x}+\chi_{\mathrm{ee}}^{xy} \kappa_{y})+ i\frac{1}{2}\kappa_{0}^{2}(\chi_{\mathrm{em}}^{xx} \kappa_{y}-\chi_{\mathrm{em}}^{xy} \kappa_{x})
\\
-\kappa_{y}\kappa_{2}+i\frac{1}{2}\kappa_{0}h_{1}(\chi_{\mathrm{ee}}^{yx} \kappa_{x}+\chi_{\mathrm{ee}}^{yy} \kappa_{y})+ i\frac{1}{2}\kappa_{0}^{2}(\chi_{\mathrm{em}}^{yx} \kappa_{y}-\chi_{\mathrm{em}}^{yy} \kappa_{x})
\end{array} \right ]
\left[\begin{array}{l}
a_{1}\\
a_{2} \\
a_{1}^{\prime}\\
a_{2}^{\prime}\\
\end{array}\right]=
\nonumber \\ %%%%%%%%%%%%%%%%%%%%%%%%%
& \left[\begin{array}{l}
-(i \kappa_{x}+\frac{1}{2}\kappa_{0}(\chi_{\mathrm{me}}^{xx} \kappa_{y}-\chi_{\mathrm{me}}^{xy} \kappa_{x})-\frac{1}{2} h_{1}(\chi_{\mathrm{mm}}^{xx} \kappa_{x}-\chi_{\mathrm{mm}}^{xy} \kappa_{y}))\\
-(i \kappa_{y}+\frac{1}{2}\kappa_{0}(\chi_{\mathrm{me}}^{yx} \kappa_{y}-\chi_{\mathrm{me}}^{yy} \kappa_{x})-\frac{1}{2} h_{1}(\chi_{\mathrm{mm}}^{yx} \kappa_{x}+\chi_{\mathrm{mm}}^{yy} \kappa_{y}))\\
-(-\kappa_{y}h_{1} + i\frac{1}{2}\kappa_{0}(\chi_{\mathrm{ee}}^{xx} \kappa_{y}-\chi_{\mathrm{ee}}^{xy} \kappa_{x})+\frac{1}{2}i h_{1}\kappa_{0}(\chi_{\mathrm{em}}^{xx} \kappa_{x}+\chi_{\mathrm{em}}^{xy} \kappa_{y}))\\
-(\kappa_{x}h_{1} + i\frac{1}{2}\kappa_{0}(\chi_{\mathrm{ee}}^{yx} \kappa_{y}-\chi_{\mathrm{ee}}^{yy} \kappa_{x})+\frac{1}{2}i h_{1}\kappa_{0}(\chi_{\mathrm{em}}^{yx} \kappa_{x}+\chi_{\mathrm{em}}^{yy} \kappa_{y}))
\end{array}\right]
\end{align}
\end{strip}
\lipsum[1]
\end{document}
خروجی:

موفقتر باشین.